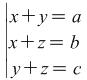
Linear cyclic systems
Aim: This topic aims at extending the knowledge students have about systems of equations and forming skills for solving them in extracurricularly in the eighth grade.
Systems of the following form
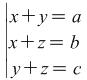
|
(1) |
and
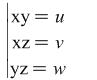
|
(2) |
or ones reduced to these two types will be called linear cyclic systems. Here ![]() are unknowns and
are unknowns and ![]() are given constants.
are given constants.
Analyzing system (1) we find the unknown quantities occur as summands in the left sides of the equations constituting it the same number of times, i.e.. they reoccur twice. Even if we change the places of the unknowns in each of the equations the system does not change its type and also contains the unknown quantities twice. This gives rise to the idea that adding together both sides of these equations we get for both cases
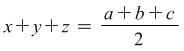
|
(3) |
Using consecutively the first, second and third equation of the system and equation (3) we realize that
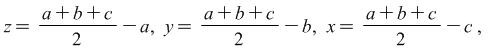
|
i.e.
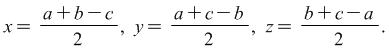
|
Think whether the solution of the system would change if we changed ![]() with
with ![]() ,
, ![]() with
with ![]() and
and ![]() with
with ![]() .
.
Analyzing system (2) we discover that here ![]() are multipliers which are also repeated twice and the system does not change its type if we change the places of the unknowns in each its equations. This suggests the idea of multiplying together both sides of the equation. We get
are multipliers which are also repeated twice and the system does not change its type if we change the places of the unknowns in each its equations. This suggests the idea of multiplying together both sides of the equation. We get ![]() , after which
, after which ![]() is found. Using the result for
is found. Using the result for ![]() and each of the equations of (2)
and each of the equations of (2) ![]() are easily found.
are easily found.
Some of the systems in this group contain a cubic equation or one with a higher exponent, but as the way to solve them requires only knowledge about how to solve linear equation systems, linear cyclic systems would be easy to cope with.
Example 1. Solve the system:
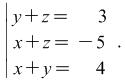
|
(4) |
This system is of the type (1), that is why we add together the sides of the equations in system (4). We get ![]() .
.
From the conditions we know that ![]() . Then
. Then ![]() i.e.
i.e. ![]() . From
. From ![]() we get that
we get that ![]() and from
and from ![]() we find
we find ![]() . The ordered triple found (-2;6;-3) is the solution to (4).
. The ordered triple found (-2;6;-3) is the solution to (4).
Knowing the solution of system (4) find the solutions to the following two systems:
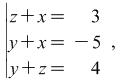
|
(5) |
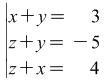
|
(6) |
without solving them.
Example 2. Solve the system
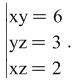
|
(7) |
Hint : The system is of the type (2) After multiplying together the equations in (7) we get ![]()
After which the solutions to (7) are found: (2;3;1), (-2;-3;-1).
Example 3. Without solving the system
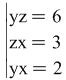
|
(8) |
find its solutions.
These ideas for solving system (1) and (2) can be used for solving the following problems:
Example 4. Solve the system
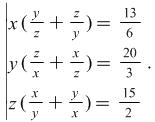
|
(9) |
In system (9) ![]() are not equal to zeros. We write (9) down in the form
are not equal to zeros. We write (9) down in the form
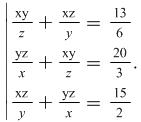
|
(10) |
System (10) is similar to (1). Then we use already known way of solving - adding together each member of the equations. We get
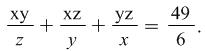
|
(11) |
By means of equations (10) and (11) we have
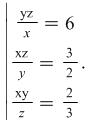
|
(12) |
This system (12) is of the type (2). It is solved using multiplication of the equations, i.e. ![]() and in combination with each equation of (12) we find that
and in combination with each equation of (12) we find that
|
|
from where it is easy to find the ordered triples of numbers which are solutions to (9)
|
|
Problem 1.
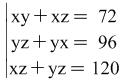 .
.
Hint: The system is of type (1). After suitable transformations it is reduced to the following system
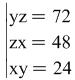
|
i.e. to a system of type (2).
Problem 2.
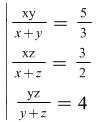 .
.
Hint: After determining what values ![]() and
and ![]() can assume present the system in the following form
can assume present the system in the following form
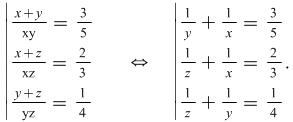
|
(13) |
System (13) is of type (1).
Problem
3. 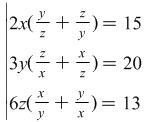 .
.
Hint: After dividing the first equation by 2, the second by 3, and the third by 6 the system is reduced to type (1) (see Example 3 above).
Problem
4. 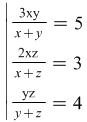 .
.
Hint: Represent the system in this way 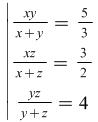 .
.
Use the hint for Problem 1.
Answers: (![]()
Problem
5. 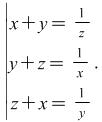
Hint: As ![]() are different from 0, the system is of the following type
are different from 0, the system is of the following type 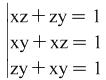 .
.
See the hint for Problem 4 above.
Problem
6. 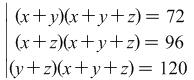 .
.
Hint: We add together each member of the equations. We get ![]() after which we will get a system of type (1).
after which we will get a system of type (1).
Problem
7. 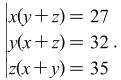
Hint: Open the brackets in each of the equations of the system. The system which we get is of type (1).
By Rumyana Mavrova, Plovdiv university, rummav@pu.acad.bg